Geometry equations, encompassing 2D and 3D shapes, are fundamental tools for calculating properties like perimeter, area, volume, and surface area – essential for diverse applications.

What is Geometry?
Geometry is a branch of mathematics concerned with the properties and relations of points, lines, surfaces, solids, and higher dimensional analogs. It’s a deeply historical field, with roots tracing back to ancient civilizations, notably the Greeks like Pythagoras, whose theorem remains foundational.
Essentially, geometry provides a framework for understanding spatial relationships. It’s not merely about abstract shapes; it’s a practical discipline used in architecture, engineering, art, and even computer graphics. The study involves defining shapes, measuring their properties, and exploring how they interact. Equations are the language used to precisely describe these relationships, allowing for calculations and predictions about geometric figures.
Conformal geometry, a specialized area, focuses on transformations preserving angles, linking geometry with complex analysis.
Importance of Geometry Equations
Geometry equations are crucial because they translate visual concepts into quantifiable data, enabling precise calculations of area, volume, and other essential properties. These equations aren’t confined to theoretical mathematics; they underpin numerous real-world applications.
Architects rely on them for building design and structural integrity, while engineers use them in constructing bridges, roads, and machines. Furthermore, fields like computer graphics and game development heavily depend on geometric equations to render realistic 3D environments.
Understanding these equations allows for problem-solving in diverse scenarios, from determining material quantities to optimizing spatial arrangements. Even advanced concepts like multipeakon solutions rely on these foundational principles.

Basic 2D Geometric Shapes & Equations
Two-dimensional geometry focuses on shapes like rectangles, triangles, circles, and parallelograms, utilizing equations to define their perimeter, area, and relationships.
Rectangle & Square Equations
Rectangles and squares, foundational shapes in geometry, possess straightforward equations for calculating key properties. A rectangle’s perimeter (P) is determined by adding all sides: P = 2ℓ + 2w, where ℓ represents length and w represents width. Its area (A) is simply length multiplied by width: A = ℓw.
Squares, being special rectangles with equal sides (s), simplify these equations. The perimeter becomes P = 4s, and the area is A = s2. These formulas are crucial for various applications, from calculating room dimensions to determining the amount of material needed for construction projects. Understanding these basic equations provides a solid base for tackling more complex geometric problems.
Perimeter of a Rectangle/Square
The perimeter, representing the total distance around a two-dimensional shape, is calculated differently for rectangles and squares, though related. For a rectangle, the perimeter (P) is found by summing all sides: P = 2ℓ + 2w, where ℓ denotes length and w denotes width. This essentially doubles the sum of length and width.
A square, possessing four equal sides (s), simplifies this calculation. The perimeter is simply four times the length of one side: P = 4s. Both formulas are fundamental in practical applications, such as fencing a garden (rectangle) or framing a square picture. Accurate perimeter calculation is vital for determining material quantities.
Area of a Rectangle/Square
Determining the area – the space enclosed within a two-dimensional shape – differs for rectangles and squares. A rectangle’s area (A) is calculated by multiplying its length (ℓ) by its width (w): A = ℓw. This represents the number of unit squares that can fit inside the rectangle.
For a square, with all sides equal (s), the area is found by squaring the side length: A = s2. This is a special case of the rectangle formula where length and width are identical. Area calculations are crucial in scenarios like flooring, tiling, or calculating the size of a wall to be painted, ensuring accurate material estimation.
Triangle Equations
Triangles, fundamental in geometry, require specific equations to determine their key properties. Calculating the perimeter (P) is straightforward: sum the lengths of all three sides – P = a + b + c, where a, b, and c represent the side lengths; However, finding the area (A) necessitates knowing the base (b) and height (h).
The standard formula for a triangle’s area is A = 1/2 * b * h. The height must be perpendicular to the base. Understanding these equations is vital in fields like architecture, engineering, and surveying, enabling precise calculations for structural designs and land measurements.
Perimeter of a Triangle
The perimeter of a triangle represents the total distance around its exterior. It’s calculated by simply adding the lengths of all three sides together. If the sides of a triangle are denoted as ‘a’, ‘b’, and ‘c’, the formula for its perimeter (P) is expressed as: P = a + b + c.
This fundamental equation is crucial in various applications, from constructing fences to determining the amount of material needed for triangular frameworks. Understanding this concept provides a foundational understanding of geometric measurement and is essential for solving more complex problems involving triangles.
Area of a Triangle
The area of a triangle defines the amount of two-dimensional space enclosed within its boundaries. The most common formula for calculating the area (A) requires knowing the base (b) and the height (h) of the triangle. The formula is: A = 1/2 * b * h. The height is the perpendicular distance from the base to the opposite vertex.
This calculation is vital in fields like land surveying, architecture, and engineering. Accurately determining a triangle’s area allows for precise calculations of land size, material requirements, and structural design. Mastering this formula is a cornerstone of geometric understanding and problem-solving.
Circle Equations
A circle, defined by all points equidistant from a central point, possesses key equations for calculating its circumference and area. The circumference (C), representing the distance around the circle, is calculated using the formula: C = 2πr, where ‘r’ denotes the radius; The area (A), representing the space enclosed within the circle, is determined by: A = πr2.
These equations are foundational in various applications, including engineering, physics, and computer graphics. Understanding these relationships allows for precise calculations related to circular objects and systems. The constant π (pi) is crucial, representing the ratio of a circle’s circumference to its diameter.
Circumference of a Circle
The circumference of a circle, essentially its perimeter, represents the total distance around its curved boundary. It’s calculated using the formula C = 2πr, where ‘C’ signifies circumference, ‘π’ (pi) is a mathematical constant approximately equal to 3.14159, and ‘r’ represents the radius of the circle – the distance from the center to any point on the circle’s edge.
Alternatively, knowing the diameter (d) – the distance across the circle through its center – the circumference can also be found using C = πd. This equation is vital in numerous practical applications, from determining the length of fencing needed to enclose a circular garden to calculating wheel rotations.
Area of a Circle
The area of a circle defines the amount of space enclosed within its circular boundary. It’s determined using the formula A = πr2, where ‘A’ denotes area, ‘π’ (pi) remains the mathematical constant approximately equal to 3.14159, and ‘r’ signifies the radius of the circle – the distance from the center to any point on the circumference.
This formula highlights that the area is directly proportional to the square of the radius. Understanding this is crucial for applications like calculating the amount of material needed to cover a circular surface or determining the capacity of a circular pool. The area is always expressed in square units.
Parallelogram Equations
A parallelogram is a quadrilateral with opposite sides parallel and equal in length. Calculating its properties involves specific equations. The perimeter (P) is found by summing all sides: P = 2a + 2b, where ‘a’ and ‘b’ represent the lengths of adjacent sides. This reflects the equal length of opposite sides.
Determining the area requires the base and height. The area (A) is calculated as A = base × height. Crucially, the height is the perpendicular distance between the base and its opposite side, not the length of the slanted side. These equations are vital in land surveying and architectural design.
Perimeter of a Parallelogram
The perimeter of a parallelogram represents the total distance around its outer edges. Since opposite sides of a parallelogram are equal in length, calculating the perimeter is straightforward. If ‘a’ and ‘b’ denote the lengths of adjacent sides, the formula is expressed as: P = 2a + 2b. This simply means adding up the lengths of all four sides.
Understanding this equation is crucial for practical applications like fencing a parallelogram-shaped garden or determining the amount of trim needed for a parallelogram-shaped room. It’s a fundamental concept in geometry, easily applied with basic addition skills.
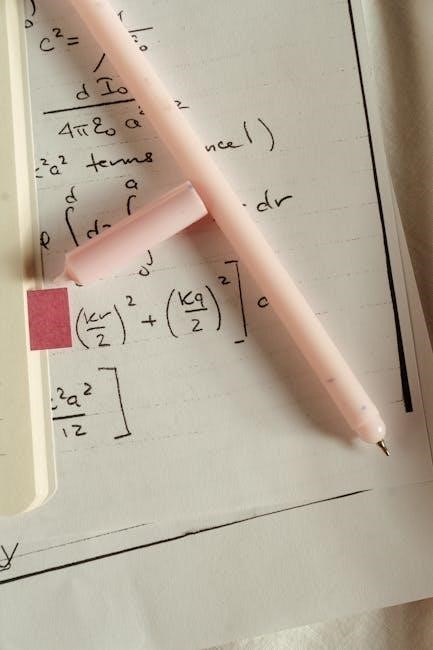
3D Geometric Shapes & Equations
Three-dimensional geometry extends 2D concepts to volume and surface area, utilizing equations for shapes like cubes, spheres, cylinders, and cones.
Cube & Cuboid Equations
Cubes and cuboids, foundational 3D shapes, possess distinct equations for calculating their volume and surface area. A cube, with all sides equal (s), has a volume (V) determined by V = s3. Its surface area (S.A.) is calculated as 6s2, representing the total area of its six square faces.
A cuboid, or rectangular prism, extends this concept with varying length (l), width (w), and height (h). The volume of a cuboid is V = lwh, while its surface area is S.A. = 2lw + 2lh + 2wh. These formulas are crucial in various fields, from architecture to engineering, enabling precise calculations of spatial requirements and material usage.
Volume of a Cube/Cuboid
Determining the volume of a cube or cuboid signifies the amount of space enclosed within its boundaries. For a cube, where all sides measure ‘s’, the volume is straightforwardly calculated as V = s3 – side multiplied by itself three times. This represents a perfect cubic unit of measurement.
However, a cuboid, possessing distinct length (l), width (w), and height (h), requires a slightly different approach; Its volume is found by multiplying these three dimensions together: V = lwh. Understanding these formulas is vital for applications ranging from calculating container capacity to determining the amount of material needed for construction projects.
Surface Area of a Cube/Cuboid
Calculating the surface area of a cube or cuboid involves finding the total area covering all its faces. A cube, with six identical square faces, each having an area of s2, yields a total surface area of 6s2. This represents the total exterior space of the cube.
For a cuboid, possessing differing length (l), width (w), and height (h), the calculation is more nuanced. It requires summing the areas of all six rectangular faces: 2(lw + lh + wh). This formula accounts for the unique dimensions of each face, providing the total exterior surface area of the cuboid.
Sphere Equations
A sphere, a perfectly round geometrical object, is defined by its radius (r). Key equations determine its characteristics. The volume of a sphere, representing the space it occupies, is calculated using the formula V = (4/3)πr3. This equation demonstrates the proportional relationship between volume and the cube of the radius.
Equally important is the surface area, representing the total area covering the sphere’s exterior, calculated as S.A. = 4πr2. This formula highlights the proportional relationship between surface area and the square of the radius. These equations are fundamental in various fields, from physics to engineering.
Volume of a Sphere
Determining the volume of a sphere is crucial in numerous applications, from calculating the capacity of spherical tanks to understanding astronomical bodies. The formula, V = (4/3)πr3, elegantly defines this volume, where ‘V’ represents volume and ‘r’ signifies the sphere’s radius.
This equation reveals a direct cubic relationship: doubling the radius increases the volume by a factor of eight. Understanding this proportionality is key to solving related problems. The constant π (pi), approximately 3.14159, is integral to the calculation, reflecting the sphere’s circular nature. Accurate radius measurement is vital for precise volume determination.
Surface Area of a Sphere
Calculating the surface area of a sphere is essential in fields like material science and physics, determining the amount of material needed to cover a spherical object. The formula, S.A. = 4πr2, provides a straightforward method, where ‘S.A.’ denotes surface area and ‘r’ represents the radius.
This equation demonstrates a quadratic relationship: doubling the radius quadruples the surface area. The constant π (pi) again highlights the sphere’s circular foundation. Unlike volume, surface area is a two-dimensional measurement, expressed in square units. Accurate radius measurement remains paramount for precise calculations, impacting applications from coating calculations to heat transfer analysis.
Cylinder Equations

Cylinder equations are crucial for understanding and quantifying three-dimensional space occupied by these common shapes; A cylinder, defined by two parallel circular bases connected by a curved surface, requires distinct formulas for volume and area calculations.
The volume of a cylinder is calculated as V = πr2h, where ‘r’ is the radius of the base and ‘h’ is the height. For surface area, we differentiate between lateral and total surface area. The lateral area (L.A.) is 2πrh, representing the curved side, while the total surface area (S;A.) is 2πr2 + 2πrh.
Volume of a Cylinder
Determining the volume of a cylinder is a fundamental calculation in geometry, representing the amount of three-dimensional space it encloses. This is particularly useful in various real-world applications, from calculating container capacity to engineering design.
The formula for calculating the volume (V) is elegantly simple: V = πr2h. Here, ‘π’ (pi) is a mathematical constant approximately equal to 3.14159, ‘r’ represents the radius of the circular base, and ‘h’ denotes the height of the cylinder. Essentially, you multiply the area of the base (πr2) by the height to find the total volume.
Lateral Area of a Cylinder
The lateral area of a cylinder refers to the area of its curved surface, excluding the top and bottom circular bases. Calculating this area is crucial in scenarios where you need to determine the amount of material required to cover the cylindrical surface, like for labeling or painting.
The formula to compute the lateral area (L.A.) is L.A. = 2πrh. Here, ‘π’ represents the mathematical constant pi (approximately 3.14159), ‘r’ signifies the radius of the circular base, and ‘h’ denotes the height of the cylinder. This formula essentially calculates the circumference of the base (2πr) and multiplies it by the height, giving the area of the rolled-out lateral surface.
Surface Area of a Cylinder
The surface area of a cylinder encompasses the total area covering its entire exterior – including both circular bases and the curved lateral surface. Determining this value is vital when calculating the amount of material needed to completely enclose a cylindrical object, such as for manufacturing or coating purposes.
The formula for calculating the total surface area (S.A.) is S.A. = 2πr² + 2πrh. This comprises two parts: 2πr², representing the combined area of the two circular bases, and 2πrh, which is the lateral area as previously defined. ‘π’ is pi, ‘r’ is the radius, and ‘h’ is the height. Adding these components provides the complete exterior surface area of the cylinder.
Cone Equations
A cone, a three-dimensional shape tapering smoothly from a circular base to a point called the apex, requires specific equations to define its properties. Understanding these equations is crucial in fields like architecture, engineering, and computer graphics for modeling and analyzing conical structures.
Key equations involve calculating its volume and surface area. The volume (V) of a cone is determined by V = (1/3)πr²h, where ‘r’ represents the radius of the circular base and ‘h’ is the perpendicular height. The surface area encompasses the base area (πr²) plus the lateral area (πrl), where ‘l’ is the slant height. Therefore, the total surface area is πr² + πrl.
Volume of a Cone
Determining the volume of a cone is a fundamental calculation in geometry, representing the amount of space enclosed within the three-dimensional shape. This calculation is vital in various applications, from calculating the capacity of conical tanks to understanding the geometry of architectural designs.
The formula for calculating the volume (V) of a cone is V = (1/3)πr²h. Here, ‘π’ (pi) is a mathematical constant approximately equal to 3.14159, ‘r’ denotes the radius of the circular base, and ‘h’ represents the perpendicular height of the cone – the distance from the apex to the center of the base. Applying this formula accurately requires correct identification of ‘r’ and ‘h’.
Surface Area of a Cone
Calculating the surface area of a cone involves determining the total area covering its exterior, encompassing both the circular base and the curved lateral surface. This calculation is crucial in fields like manufacturing, where material requirements need precise estimation, and in understanding spatial properties.
The total surface area (TSA) is found using the formula: TSA = πr² + πrl, where ‘π’ is approximately 3.14159, ‘r’ is the radius of the base, and ‘l’ represents the slant height – the distance from the apex to any point on the circumference of the base. The slant height can be calculated using the Pythagorean theorem if the height (h) and radius (r) are known: l = √(r² + h²). Accurate measurement of ‘r’ and ‘h’ is essential for precise results.
Pyramid Equations
Pyramids, characterized by triangular faces meeting at a common vertex, require specific equations to determine their spatial properties. Understanding these equations is vital in architecture, engineering, and various mathematical applications. Calculating the volume and surface area are key aspects of pyramid geometry.
The volume of a pyramid is calculated using the formula: V = (1/3) * Base Area * Height. The ‘Base Area’ depends on the shape of the base (square, rectangle, triangle, etc.). The surface area calculation involves summing the area of all faces – the base and the triangular sides. Precise measurements of base dimensions and height are crucial for accurate results, enabling effective spatial analysis and design.
Volume of a Pyramid
Determining the volume of a pyramid is fundamental in geometry, representing the amount of space enclosed within its boundaries. The formula, V = (1/3) * Base Area * Height, elegantly captures this relationship. The ‘Base Area’ is calculated based on the pyramid’s base shape – square, rectangular, or triangular – requiring appropriate area formulas.
Accurate measurement of both the base area and the perpendicular height (from the apex to the base) is critical for precise volume calculation. This formula applies to all pyramid types, making it a versatile tool. Understanding this equation is essential for applications in architecture, engineering, and mathematical modeling, allowing for efficient spatial analysis and resource estimation.

Fundamental Geometric Theorems & Equations
Key theorems, like the Pythagorean Theorem, and principles of conformal geometry, underpin geometric calculations, establishing vital relationships between angles, shapes, and equations.

Pythagorean Theorem
The Pythagorean Theorem, a cornerstone of geometry attributed to the ancient Greek mathematician Pythagoras, defines the relationship between the sides of a right-angled triangle. Specifically, the theorem states that the sum of the squares of the two shorter sides (legs or catheti – often denoted as ‘a’ and ‘b’) is equal to the square of the longest side (the hypotenuse – denoted as ‘c’).
This fundamental principle is expressed mathematically as: a² + b² = c². It’s not merely an abstract equation; it has practical applications in numerous fields, including construction, navigation, and surveying. Understanding this theorem is crucial for solving problems involving right triangles, calculating distances, and verifying angles. The theorem’s enduring relevance stems from its simplicity and broad applicability across mathematical disciplines and real-world scenarios.
Conformal Geometry & Equations
Conformal geometry delves into transformations that preserve angles locally, offering a unique perspective within geometric studies. Unlike traditional geometry focused on lengths and distances, conformal geometry prioritizes the preservation of shapes, making it invaluable in diverse fields like complex analysis and physics. These transformations, known as conformal mappings, are often described by complex-valued functions.
The interplay between conformal geometry and nonlinear elliptic equations reveals deep interrelations between geometry and analysis. These equations, characterized by their complexity, often arise when studying conformal mappings and their properties. Understanding these connections allows for solving problems in areas like fluid dynamics and electrostatics, where conformal mappings provide powerful analytical tools.
Advanced Geometry Equations
Advanced geometry explores complex calculations, including polyhedra volumes and multipeakon solutions—challenging areas requiring sophisticated mathematical techniques and specialized formulas.
Volume of Polyhedra
Calculating the volume of polyhedra, shapes with flat polygonal faces, represents a classical geometry problem with roots in ancient mathematics and continuing relevance today. Unlike simpler forms, a single universal formula doesn’t exist; the approach depends heavily on the specific polyhedron’s complexity.
For regular polyhedra – like cubes or tetrahedra – established formulas are readily available. However, irregular polyhedra often require decomposition into simpler shapes—pyramids, prisms, or tetrahedra—whose volumes are individually calculated and then summed. This decomposition strategy allows for manageable computation.
Furthermore, vector calculus and coordinate geometry provide alternative methods for determining volume, particularly useful for complex, non-convex polyhedra. Understanding these techniques is crucial in fields like computer graphics, architecture, and engineering, where precise volume calculations are paramount.
Multipeakon Solutions
Multipeakon solutions represent a fascinating area within advanced geometry, specifically concerning wave propagation and nonlinear equations. Previously known solution formulas were limited, covering only scenarios where all wave amplitudes were non-zero, relying heavily on inverse spectral methods. This restriction hindered a complete understanding of multipeakon behavior.
Recent advancements aim to overcome these limitations, exploring techniques beyond inverse scattering. These methods seek to describe solutions with varying amplitude characteristics, including those where some peaks may diminish or disappear entirely.
The study of multipeakon solutions is crucial for modeling complex physical phenomena, such as rogue waves in oceans or nonlinear optical pulses, demanding sophisticated mathematical tools and a deeper understanding of the underlying geometric principles.

Leave a Reply
You must be logged in to post a comment.